Random Sampling inside a Sphere
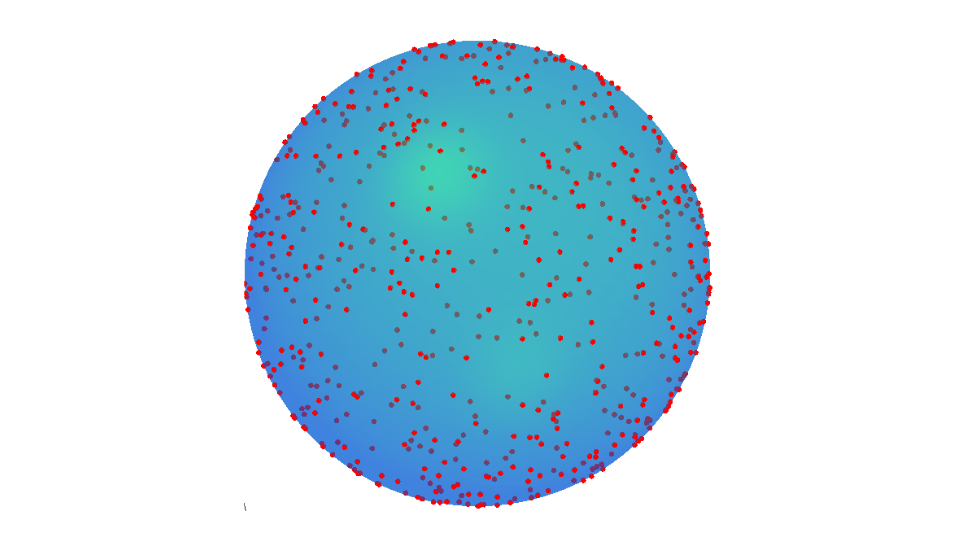
How do we randomly sample a point inside a sphere? This is a problem I’ve encountered more than once in my work (and in an interview, too!). Occasionally I’d forget the formula or how to arrive at it, so I decide to write a blog post that details this interesting problem.
If you haven’t seen this problem before, note that “randomly” here implies uniform distribution, which means every spot inside the sphere is equally likely to be picked. To solve this problem, you’re usually given a random number generator (RNG) that uniformly outputs a number in .
We’ll start with the easier 2D version of this problem: randomly sample a point inside a circle. We’ll assume the origin of the circle is at , and the radius is .
0. The Wrong Approach
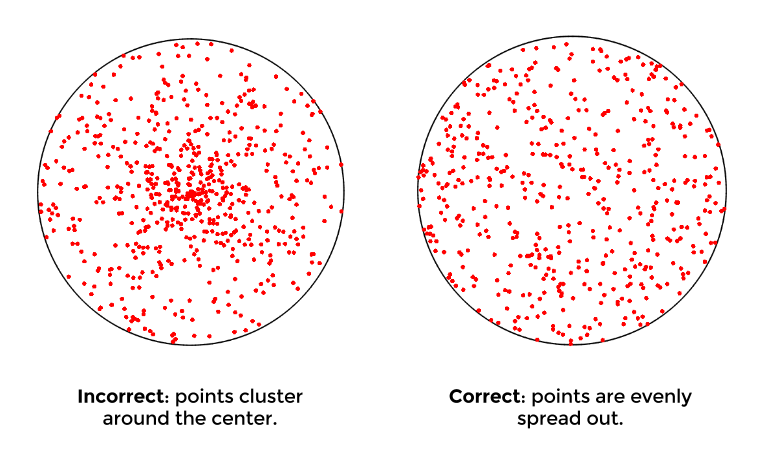
The most intuitive thing to do is to generate a random point via polar coordinates: using the uniform RNG, generate a random in and a random in .
Visualizing the results, you’ll notice that points will cluster around the center, which is not desired. The reason this happens: imagine there are 2 rings on this circle, and . is formed by , and has . Even though the area of is clearly larger than , the two rings are equally likely to be picked. Therefore, the density of points in will be lower than .
There are a couple of methods to properly sample uniform points on a circle, and they are listed below.
1. Rejection Sampling
The first approach is simple: we randomly sample a point inside a square that encloses the circle (random and in ), and discard any point outside the circle.
This is called rejection sampling. It’s fast and reliable in practice; the only problem is that it’s undeterministic, which means you might get unlucky and hit 100 out-of-circle points in a row, even though the probability of that is astronomically small.
2. Random Point inside a Small Triangle
The second approach switches back to polar coordinates: once we pick a random , we can treat the selected slice as an infinitesimal triangle , with as the origin and & on the border. The three sides of this triangle are: , , and . Now we can convert this problem into random point picking on a triangle.
By generating a random on and a random on (both in ), we can form a quadrilateral and use as our random point. If is outside the triangle, we fold it back.
In fact, since is next to 0, all four points of the quadrilateral are virtually on the same line, and we simply sum up and to generate the random point (and fold it back if needed).
3. Inverse CDF
The third approach again uses polar coordinates, but this time we’ll take a closer look at the area of the circle to develop a more general approach.
Since an infinitesimal area of the circle is
we can tell that the area of a small piece of the circle is proportional to the radius. Because we want our “sampling density” to match this distribution, you can imagine that the probability density function (PDF) would be in the form of:
The cumulative distribution function (CDF) is thus
We can compute & with the definition of CDF:
It’s great that we have the PDF and CDF of our desired distribution, but how do we generate random variables with this particular distribution, when all we have is a uniform RNG?
Well, it turns out that in statistics, there’s a handy method to achieve this: probabilty integral transform. It basically means that, an arbitrary continuous random variable can be transformed into a uniform random variable, and vice versa.
So, if we have as a uniform random variable, and being an arbitrary random variable (it could be Gaussian, exponential, anything), the following will hold:
The first equation means that, if we plug a random variable into its own CDF, the output would be a uniform distribution. The second equation means that, if we plug into the inverse of the CDF of , the output would be . In my opinion, these concepts are not the most intuitive ideas to grasp; this particular thread offers some great explanation.
Since our goal here is to obtain with , we’ll do exactly what the second equation suggests, and find the inverse CDF. Using as a pseudo variable:
That equation above is exactly how we’re going to generate a random : we just find the square root of our uniform random number, multiply it by , and that would be the random that achieves uniform distribution across the whole circle.
4. Random Point on a Sphere
We can now apply the approach above to the 3D case (or any N-dim case). Again, the sphere we’re looking at has its origin at with radius .
Before moving on to the problem of sampling points inside a sphere, let’s first look at sampling points on the sphere, since they are closely-related.
Using spherical coordinates, the infinitesimal surface area of the sphere is:
Here’s an image in case you don’t remeber where this equation comes from.
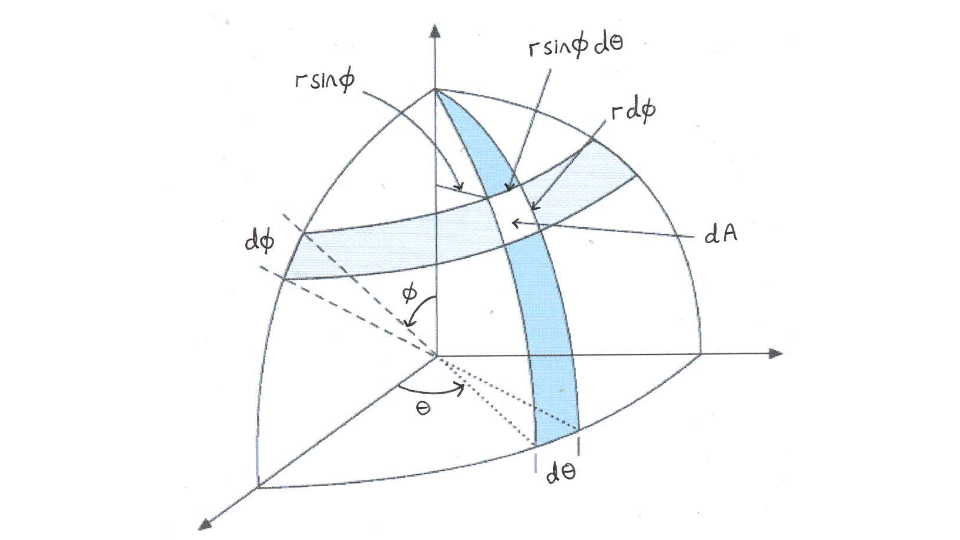
You can tell by the equation that it’s similar to the 2D case, only this time it’s proportional to instead of . (Note that here is a constant, since we’re dealing with surface area)
Using the definition of CDF, we can find out that and :
Now we can solve for the inverse CDF:
The result is plotted at the top of this article.
4. Random Point inside a Sphere
Finally, let’s look at the original problem! Sampling random points inside the sphere is simply an extension of the surface version: once we pick a random point on the surface, we can use it as a direction, and couple it with a random radius .
Similar to the 2D case, the infinitesimal volume of the sphere would depend on : (the fact that it’s instead of also makes sense, since it’s 3D now)
We can deduct the CDF with similar steps:
5. FAQ
How about we just apply rejection sampling to the 3D version?
You can. However, note that the success rate in each run is lower than the 2D version:
The volume ratio of a hypersphere (N-dim sphere) to a hypercube (N-dim cube) is one of the characteristics of curse of dimensionality.
I still don’t really understand probability integral transform. Why would plugging a random variable into its own CDF result in a uniform distribtion? What’s the intuition behind it?
Here’s my take on it: say the class takes an exam, and distribution of the scores is the exponential distribution with (don’t ask):
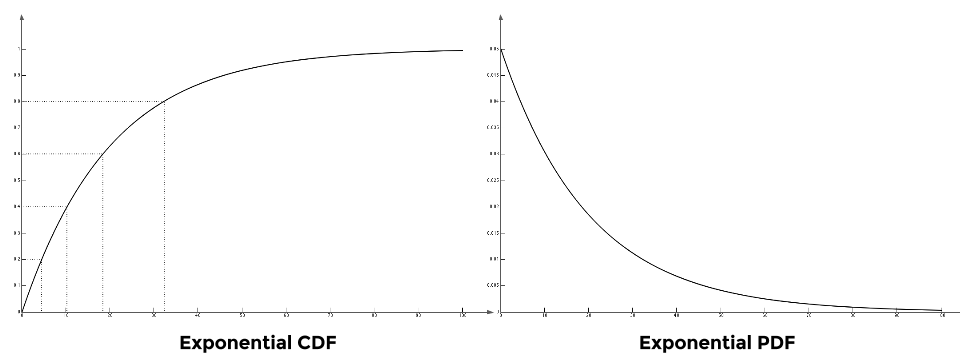
Recall that on a CDF, simply means how much percentage is below . For example, means that 77% of the students have scores lower than 30 (hey, this was actually the case in one of my undergrad course!). For simplicity’s sake, let’s divide up the CDF into 5 intervals, each with 20% on the y-axis. You can see it in the figure above.
To achieve a uniform distributed output, we want equal amount of students in each range of scores. For example, any student with score in is inside the 20% - 40% segment (orange), while scores in is inside the 60% - 80% segment (green).
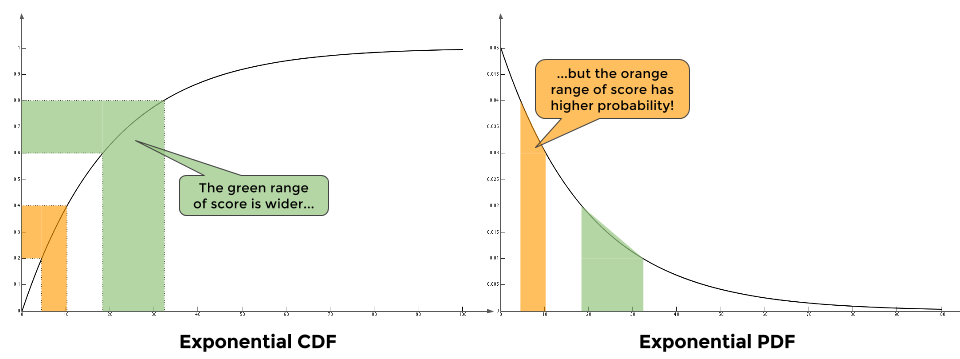
Note that the green segment has a wider range of score than the orange segment. Does that mean the score of a random student is more likely to land in the green segment instead of the orange segment? No! Becasue according the distribution of the scores on the PDF, there’re far more students having scores in than ! So the probabilty and the range sort of cancel out each other, and you would get a nice uniform distribution in the end.
